srjskam's site

There are a lot of tutorials and guides in the net on the subject of drawing ellipses, but they — invariably to my knowledge — follow the same formula: project a square in perspective, then sketch an ellipse inside it with guides.

The ghost of Euclid cries in agony every time someone draws an ellipse like that. This guide will tell you how to do it precisely using the classic tools: a ruler, a compass, and additionally a piece of string and two pins, to render the ellipse itself.

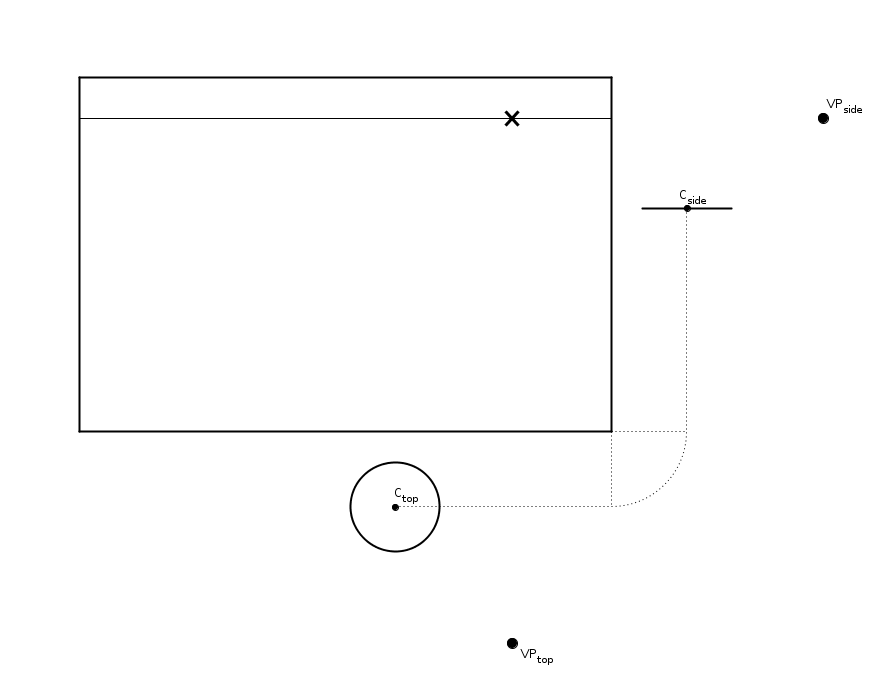
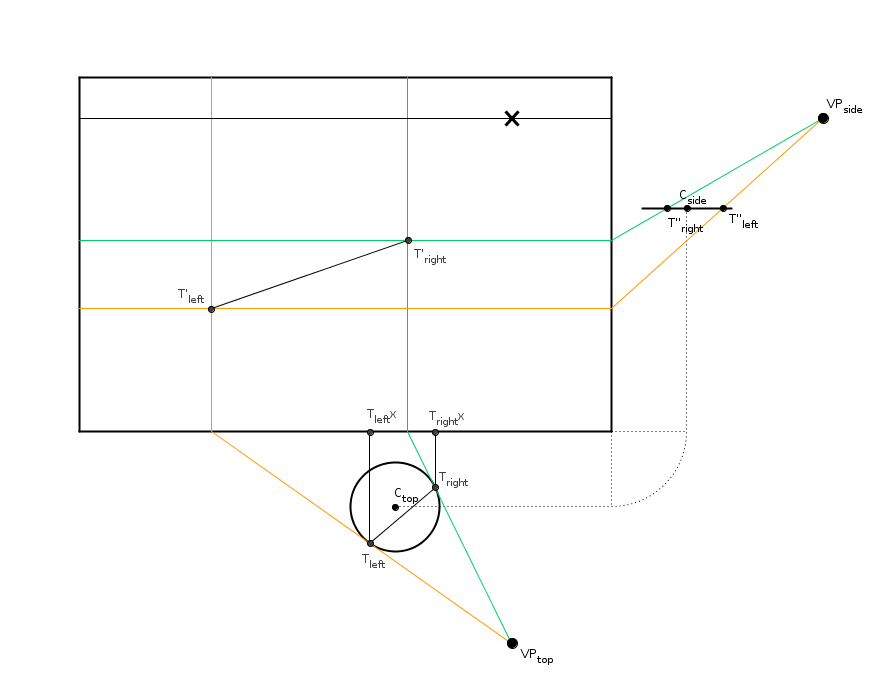
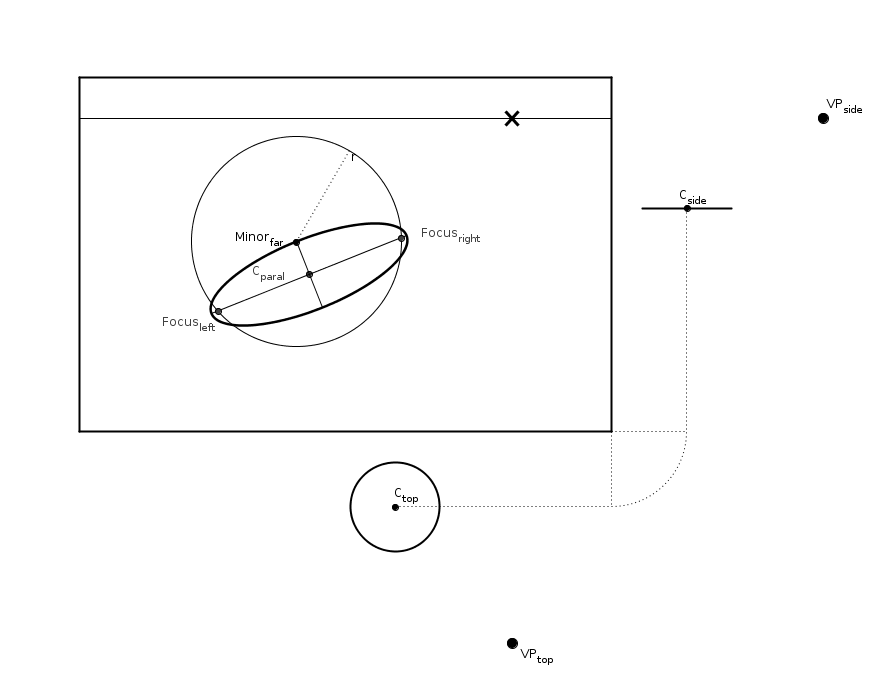
We'll start with a basic setup to project objects in perspective from a top and a side view:

Under the canvas is the top view, and on the right the side view, each with viewpoints (VP). The bottom and right segments of the canvas are used as the 2D screen to project onto. The vanishing point (marked with an X) and the horizon can be found by drawing lines parallel to the projection lines from the viewpoints.

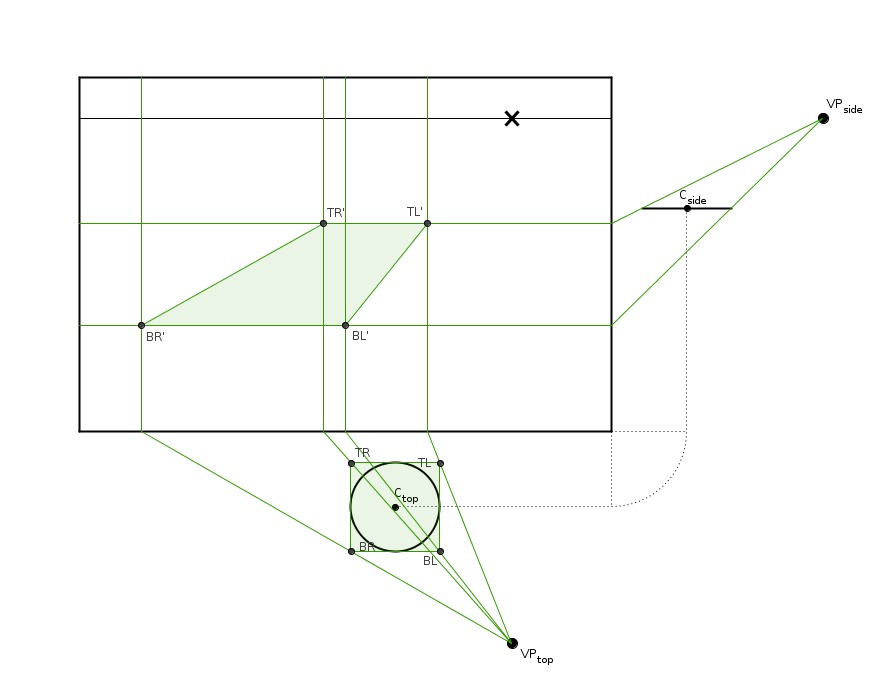
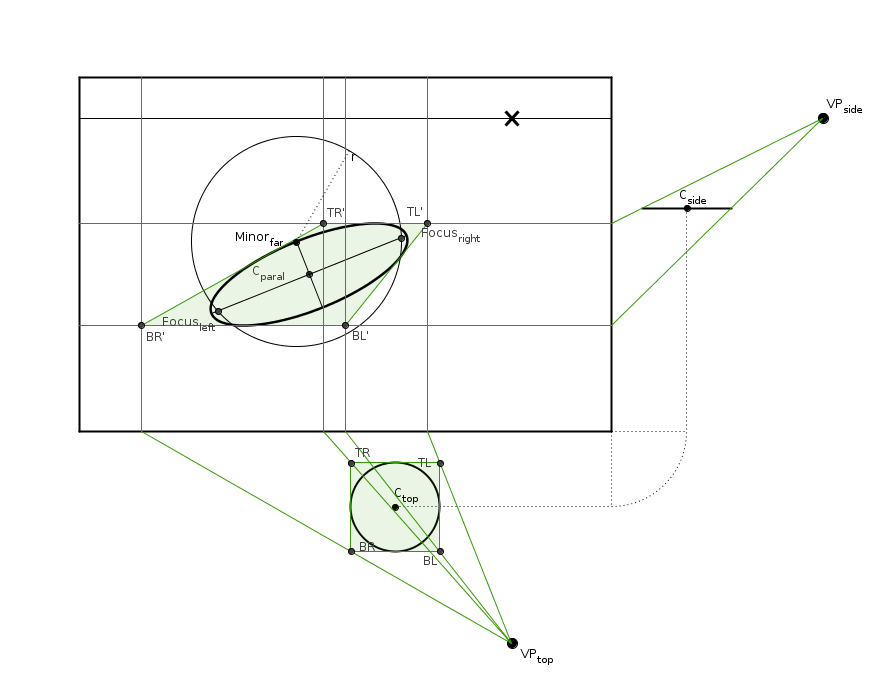
Let's start by projecting a rectangle we've drawn around the circle. This step is a red herring when using our exact method, but it'll work as an introduction to projecting in perspective and also as a reality check when we finish constructing the ellipse.

This is pretty simple. Draw rays from the viewpoints through the points you want to project. Where the rays cross the projection line (bottom and right), draw perpendicular lines across the canvas. The points can be found in the intersections of the relevant lines.

Let's put the square away and take the first steps of our method.

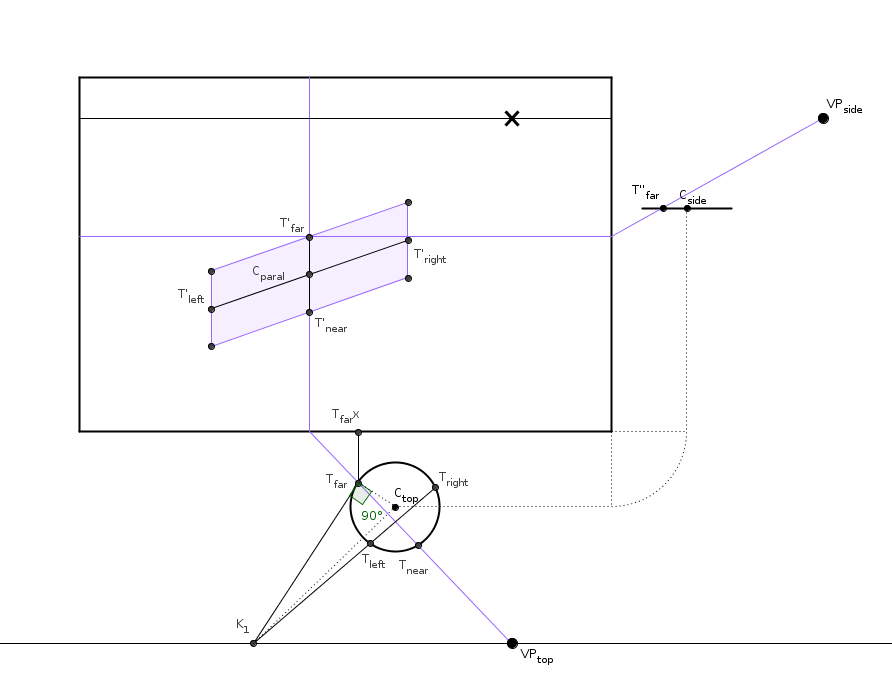
First we'll find out the leftmost and rightmost points of the ellipse on the canvas by projecting the tangent points T _left and T _right. Draw rays from the top viewpoint on the projection line across the tangent point. (You can find the tangent points by using the fact that the angle C _top - T _left - VP _top is a straight angle. You know C _top - T _left and C _top - VP _top, so you can find out T _left - VP _top using Thales's theorem.)

Measure the lengths of the tangent points from the projection line (T _left - T _leftx and T _right - T _rightx) and use them to find out the distances of the tangent points (T'' _right, T'' _left) on the side view. Project, perpendiculars, crossings, ready. We've found the tangent points and one conjugate diameter. We need another of those, so on to the next step.

Here we go about finding T' _far. T' _left and T' _right are the tangent points, so the vertical lines across them are the tangents. The smaller conjugate diameter has to be parallel to these, so it must be somewhere along the line that crosses C _paral. Now we "project backwards": draw that vertical line, and where it crosses the projection line, draw to VP _top. Now we found T _far and T _near. We only need to find one of their distance from the projection plane (T _far - T _farx) to get both points, since they are the same distance from C _paral.

We can do a sanity check by doing the same a bit harder way. You can skip this step. Honestly it's here because I didn't see the easier method before doing the graphics...

As you might have noticed, all points that go through a ray from VP _top, are projected in the same vertical line on the canvas. So, points that lie on some other ray will form a line that is parallel to the first one. Imagine drawing a bunch of rays from a single point and taking a photograph from the exact point where they converge. The rays will seem like a bunch of parallel vertical lines on the photo.

Turns out that any rays projected from some other point (like point K here) that is equally far from the projection line as your viewpoint, any rays drawn from that point will seem parallel on the canvas. We use this fact to find out T' _far.

Draw a ray from T _right through T _left to a line that goes through VP _top and is parallel to the projection line. Where it crosses, is our point K. We want to find tangent line T' _far that is parallel with T' _left - T' _right, so we draw a ray from K to T _far (that we found using the right angle triangle as before).

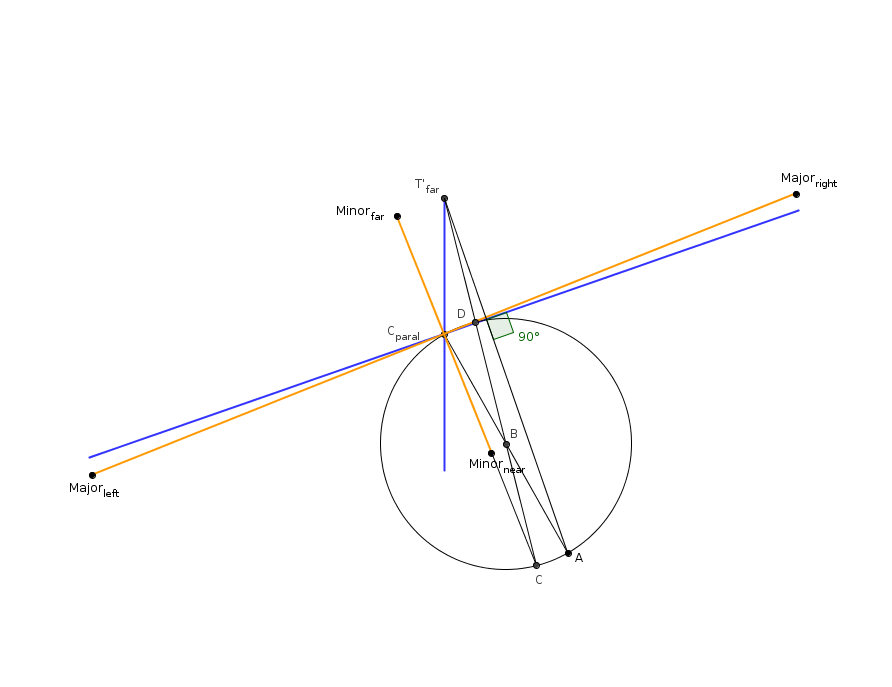
Now we have the conjugate diameters, and must find the major and minor axes of the ellipse using a procedure described in  http://www3.ul.ie/~rynnet/swconics/EP%27s.htm. (Another choice would be Rytz's construction).

The blue segments are the diameters from the previous step.

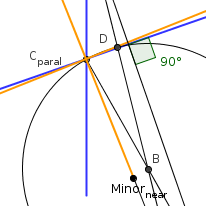
From one of the ends of the shorter diameter (T' _far) draw a segment (T' _far - A) that is as long as half of the longer diameters, perpendicular to the longer diameter.

Then a segment from A to the center (C _paral). Find the middle of this segment, call it B.

Draw a circle with the center in B, with radius A-B == B-C _paral.

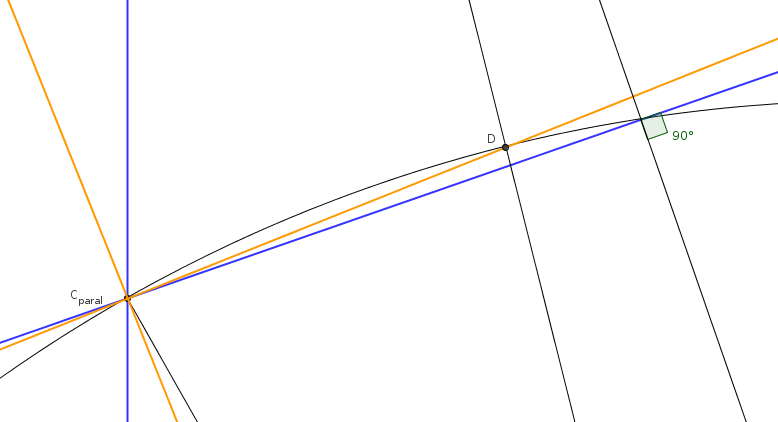
Then T' _far to C on the circle. Mark the point where this line first crosses the circle as D. The illustration is a bit messy, so here's a detail:

Now from C to C _paral. This is the direction of the minor axis.

Get the length of T' _far to D. This is the length of half of the minor axis. T' _far to A is the length of half of the major axis, and they are of course perpendicular to each other. Now we should have both the axes.

Now just take half the length of the major axis (C _paral to Major' _right or Major' _left), and draw a circle from one of the small axis points (Minor _far or Minor _near). Where it crosses the major axis (Focus _left, Focus _right) are the foci. Take your pins, stick them into these points. Measure a loop of string such that it spans Focus _left, Focus _right, and Minor _far. Stick your pen inside and draw an ellipse. Enjoy the feeling of accomplishment, shed the shame of drawing potatoes and calling them circles in perspective. May the ghost of Euclid smiles at you.

When we superimpose the square we projected in the first step, it indeed looks sane:

Now, as simple as this might seem in hindsight, this bugged me for years. There are lots of assumptions you might make that turn out wrong. I learned this the hard way. Here are all the things I tried superimposed before I found the Truth:

Everything on this page was drawn with GeoGebra. You can download the source to play with. Try moving the vanishing point, viewpoints and the circle!